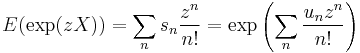Ursell function
In statistical mechanics, an Ursell function or connected correlation function, is a cumulant of a random variable. It is also called a connected correlation function as it can often be obtained by summing over connected Feynman diagrams (the sum over all Feynman diagrams gives the correlation functions).
If X is a random variable, the moments sn and cumulants (same as Ursell functions) un are related by the exponential formula:
(where E is the expectation).
The function was named after Harold Ursell, who introduced it in 1927.
References
- Glimm, James; Jaffe, Arthur (1987), Quantum physics (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96476-8, MR887102
- Ursell, H. D. (1927), "The evaluation of Gibbs phase-integral for imperfect gases", Proc. Cambridge Philos. Soc 23: 685–697, doi:10.1017/S0305004100011191